Einführung in die Programmierung: Weiterführende Programmierung

 ← zurück zur Startseite

Eingabe-Ausgabe (E/A)

• gesamter Datenaustausch von Programmen mit Speichermedien, über Netze, zwischen Threads, Prozessen sowie peripheren Geräten erfolgt einheitlich über Datenströme (engl. streams)
• Datenstrom: abstraktes Konstrukt, dessen Fähigkeit darin besteht, Zeichen auf ein imaginäres Ausgabegerät zu schreiben oder von diesem zu lesen.
• Eingabestrom: folge von Daten aus einer Daten-Quelle in ein Programm
• Ausgabestrom: Daten aus Programm in eine Daten-Senke

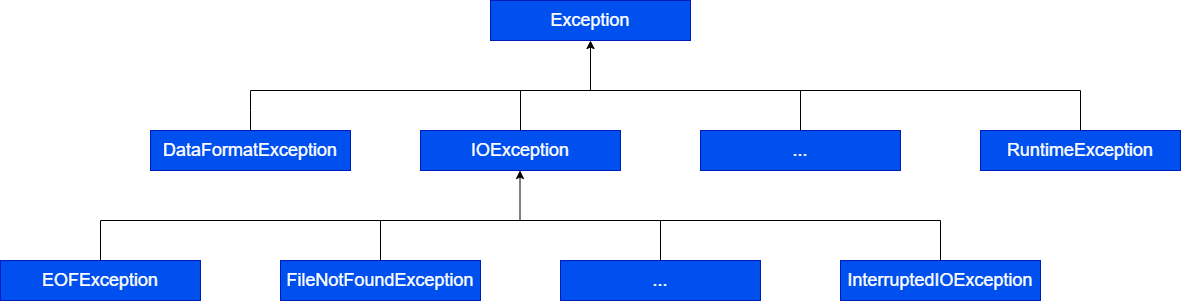
• Ausnahmefehler im Paket java.io
• alle Konstruktoren und die meisten Methoden der Klasse java.io können IOExceptions erzeugen
• eine IOException muss entweder in einer try-catch-Anweisung abgefangen oder durch eine throws-Deklaration weitergeleitet werden

 




Verkettung und Verschachtelung

• Streams können verkettet und verschachtelt werden
• Verkettung: Dateien werden zusammengefasst und für den Aufrufer als ein einziger Strom dargestellt
• Verschachtelung: erlaubt die Konstruktion von Filtern, die bei der E/A bestimmte Zusatzfunktionen (Puffern von Zeichen, Zählen von Zeilen, Interpretation binärer Daten) übernehmen
• beide Konzepte sind mit normalen Sprachmitteln realisiert und können selbst erweitert werden (eigene Filter zur Analyse des Eingabestroms)

 

Verarbeitungsprinzip von Streams

• Lesen

  öffne(Strom)
  solange (Daten zu lesen){
      lies(Daten)
      verarbeiten(Daten)
  }
  schließe(Strom)

Schreiben

  öffne(Strom)
  solange(Daten zu schreiben){
  	verarbeite(Daten)
   	schreibe(Daten)
  }
  schließe(Strom)

Ein- und Ausgabe in Java

• Das Paket java.io stellt eine umfangreiche Bibliothek für die Ein-und Ausgabe bereit (Klassen für verschiedenartige Ströme):
• Eingabeströme für Bytes: InputStream
• Ausgabeströme für Bytes: OutputStream
• Eingabeströme für Zeichen: Reader
• Ausgabeströme für Zeichen: Writer
• Interfaces für bestimmte Funktionalitäten: DataInput, DataOutput, ObjectInput, ObjectOutput, Serializeable
• Dienstklassen für spezielle Aufgaben: File, RandomAccessFile

 

Byte-Streams

• InputStream und OutputStream sind die abstrakte Superklassen für byteorientierte Datenströme
• Konstruktoren(Auswahl):
• FileInputStream, ByteArrayInputStream
• FileOutputStream
• bieten Methoden zum Lesen und Schreiben von 8-bit-Werten (Bytes)
• Verwendung insbesondere für das Lesen und Schreiben von Binärdateien
• zwei Byte-Streamklassen, ObjectInputStream und ObjectOutputStream, werden für die Objekt-Serialisierung verwendet

Die Datei

• File-Objekte repräsentieren in Java Dateien bzw. Verzeichnisse des Datei-Systems
• Sie ermöglichen Zugriff auf wichtige Dateiattribute
• haben keinen Bezug zum Datei-Inhalt (dafür sind die Dateiströme zuständig)

NIO

-> non-blocking-Input-Output (NIO)

• zentrale Klassen: FileSystem und Path
• Typen befinden sich im Paket java.nio.file
• Unterstützung des try-ressource-statements: Der Compiler kümmert sich automatisch, um das Schließen der Ressource

 

Path

• ->  repräsentiert einen Pfad bzw. eine Datei im System
• Möglichkeiten:
• Name
• (Teil-)Pfade
• Rootverzeichnis

Files

• stellt Routineoperationen (kopieren, löschen, ...) zur Verfügung

sonstige Ein-/Ausgabe

• Netzwerke
• Tastatur
• Console
• Drucker/Scanner

 

Gepufferte Ein-/Ausgabe

• Minimierung der Ein-/Ausgabe-Operationen
• Größe, die gepuffert werden soll kann angegeben werden

Beispiel:

• Eigenschaften	BufferedReader	Scanner
  Thread-Safe?	✅	❌
  beliebige Größe?	möglich	nicht möglich
  Fehlerbehandlung?	notwendig	Fehlermeldungen werden versteckt

Serialisierung

• -> Objekte werden in eine Folge von Bytes transformiert

Deserialisierung

• -> Eine Folge von Bytes werden in ein Objekt transformiert

Einsatz

• Senden über ein Netzwerk
• Speichern der Objekte in einer Datenbank

Interface

• Serializable

 

Aufwand von Algorithmen

• Wenn für einen Aufgabenklasse verschiedene Algorithmen existieren, welcher ist der beste Algorithmus?
• (mögliche) Kriterien:
• Speicheraufwand
• Speicherbedarf für Programm -> konstant
• Speicherbedarf für Dateien -> abhängig von Eingabewerten -> Speicherkomplexität
• Zeitaufwand -> abhängig von Eingabewerten -> Rechenkomplexität

 

Vorüberlegung

• Konkreter Bedarf an Speicher und Rechenzeit eines Algorithmus hängt von Implementierung in einer Programmiersprache ab und vom Rechner, der das Programm ausführt
• Genaue quantitative Aussagen sind schwierig, daher werden keine realen Laufzeiten und Speichervolumen untersucht, sondern ihre Größenordnungen in Abhängigkeit von Umfang und Art der Eingabedaten
• Idee: Idealisierung des Computers als "abstrakte Maschine", bei der alle Operationen die gleiche Zeiteinheit und alle elementaren Daten den gleichen Speicherplatz brauchen.

 

Begriffe

• Dimension (Umfang) eines Problems:
• Anzahl oder Größe n der Eingabedaten
• Aufwand eines Algorithmus:
• Anzahl T(n) von Zeit- bzw. Speichereinheiten bei seiner Durchführung für ein Problem der Dimension n
• In T(n) wird i.a. nur der am stärksten wachsende Teil betrachtet, d.h., es interessiert der asymptotische Aufwand eines Algorithmus:
• Verhalten bei n -> ∞
• Beachte: Was mit kleinen Eingabemengen noch gut funktioniert kann bei einem Anwachsen der Eingabemenge rasch zu einem Problem werden.

 

Aufwand von Algorithmen

• Zumeist ist der Aufwand auch abhängig von der Art der Eingabedaten, so unterscheidet man:
• günstigster Aufwand ("best case")
• mittlerer Aufwand ("average case")
• ungünstigster Aufwand ("worst case")
• Komplexität einer Problemklasse:
• Kleinstmöglicher Aufwand von Algorithmen, die jedes konkrete Problem dieser Klasse lösen können
• Erfordert die Angabe eines entsprechenden Algorithmus und den Nachweis, dass kein Algorithmus das Problem mit geringerem Aufwand lösen kann.

 

Beispiel:

• Aufwand für x = bas^n

  public long pot1(int bas, int n){
  	long pot = 1;
  	while (n >= 1){
  		pot = pot * bas;
  		n = n - 1;
  	}
  	return pot;
  }

 

Elemente des Codes:

• 1 Methodenaufruf
• 3 lokale Variablen bas, n, pot
• 3 Zuweisungen (line 1 + 2)
• n+1 Vergleiche (line 3)
• n Multiplikationen (line 4)
• n Subtraktionen (line 5)
• 2*n Zuweisungen (line 4 + 5)
• n+1 Sprünge (line 3 -> 6)
• 1 Rückgabe

T(n) = 1+3+3+n+1+n+n+2*n+n+1+1 = 6n +10 \in O(n)

• komplexer Aufwand für x = bas^n

  public long pot2(int bas, int n){
  	long pot1 = 1;
      while (n >= 1) {
  		if (n % 2 == 1){
          	pot = pot * bas;
          	n = n - 1;
         	}
          bas = bas * bas;
          n = n / 2;
          }
  	return pot;
  }

 

Elemente des Codes:

• 1 Methodenaufruf
• 3 lokale Variablen bas, n , pot
• 3 Zuweisungen (line 1 + 2)
• n + 1 Vergleiche (line 3)
• n-Restwerte/Modulo (line 4)
• n Vergleiche (line 4) -> ==1
• n-Sprünge (line 4 -> 7)
• n_1 Multiplikationen (line 5)
• n_1 Subtraktionen (line 6)
• 2 * n_1 Zuweisungen (line 5 + 6)l
• n Multiplikationen (line 8)
• n Divisionen (line 9)
• 2 * n Zuweisungen (line 8 +9)
• n + 1 Sprünge (line 3 -> 10)
• 1 Rückgabe

 

T(n) = 10+ 9n + 4n_1 <= 9n + 4n + 10

10+ 9n + 4n_1<= 13n + 10

Durch Zeile 9:

•  je Schleifendurchlauf wird das n (Exponent) halbiert
• n/2^k < 1 -> n < 2^k log_2 (n) < k
• max. log_2 (n)+1

T(n) = 13* (log_2 (n) + 1)+10 = 13*log_2 (n) + 23 \in \boldsymbol{O}(log n)

O-Notation

• Ziel: Möglichst einfache Klassifizierung des Aufwands für unterschiedliche Algorithmen

"O" ist eines der sog. Landau-Symbole (von E. Landau eingeführt zum Vergleich des Wachstums von Funktionen)

für Konstanten  k > 0 und für Funktionen f(n), h(n) >= 0 gilt:

1. Summen-Regel O(f(n) + O(h(n)) = O(f(n) + h(n))
   • -> jeweils nur der höchste konstante Faktor spielt eine Rolle für Komplexität des Algorithmus
2. Produktregel k* O(f(n)) = O(f(n)), O(f(n)) * O(h(n)) = O(f(n)*h(n))
   • konstante Faktoren spiele keine Rolle für die Komplexität des Algorithmus

Aufwandsklassen

1. O(1)

   -> konstanter Aufwand
   

2. O(log_2 (n))

   -> logarithmischer Aufwand
   

3. O(n)

   -> linearer Aufwand
   

4. O(n*log_2 (n))

   -> n-log(n) Aufwand
   

5. O(n^2)

   -> quadratischer Aufwand
   

6. O(n^3)

   -> kubischer Aufwand
   

7. O(e^n)

   -> exponentieller Aufwand
   

 

Suchen

Suche nach Daten

• -> Wiederbeschaffen bestimmter Informationen aus Informationsmengen ist eine zentrale Aufgabe der Datenverarbeitung

Beispiele:

• Suche einer Telefon-Nr. im Telefonbuch
• Suche einer Akte in einem Registratur
• Suche einer Datei im Datei-System
• ...

Suchen in Feldern

Wir betrachten zunächst das stark vereinfachte Problem, dass Datenstrukturen Zahlen in einem Array sind und mit ihren Schlüsselwerten identisch sind:

Dann besteht das Problem darin, in einem Zahlen-Array den Index einer vorgegebenen Zahl zu bestimmen

Falls die Zahl nicht im Array enthalten ist, soll der Wert -1 geliefert werden

Es gibt zwei prinzipielle Verfahrensweisen, je nachdem, ob das Array sortiert ist oder nicht:

• für unsortierte Arrays: lineares Durchsuchen
• für sortierte Arrays: Intervall-Teilung

 

Sequentielle/Lineare Suche

Problem: gegeben ist eine Folge F(a_1, ..., a_n)

Jedes Element muss angesehen werden bis gesuchtes Element gefunden wurde oder -1 bei keinem Treffer

Aufwand:

• günstigster Fall: k = 1 -> O(1)
• ungünstigster Fall: k = n -> O(n)
• mittlerer Fall: k = n/2 -> O(n)

 

Binären Suche für sortierte Zahlen-Arrays

Prinzip: Intervall-Teilung

• Falls das Array leer ist, gib -1 zurück
• Sonst nimm das mittlere Element des Arrays
• Falls sein Wert der gesuchte Wert ist, gib den Index des mittleren Elements zurück
• Falls sein Wert kleiner ist als der gesuchte Wert, suche im rechten Teilarray weiter
• Falls sein Wert größer ist als der gesuchte Wert, suche im linken Teilarray weiter
• Die zu untersuchenden Teilarrays werden durch zwei Indizes "von" und "bis" als Abschnitt des Gesamtarrays gekennzeichnet
• O(log_n(n))

 

Lineare vs. Binäre Suche

• Binäre Suche ist für große Datenmengen viel effizienter als Lineare Suche
• Verdoppelt sich die zu durchsuchende Datenmenge, verdoppelt sich im Fall der Lineare Suche die Anzahl der Suchschritte, bei binärer Suche hingegen wird lediglich eine einzige zusätzliche Vergleichsoperation benötigt.
• Binäre Suche hat aber Anforderungen:
• dass in der Liste alle Elemente in Position gespeichert sind,
• man über die Position direkt auf das dort befindliche Element zugreifen kann,
• eine Ordnung (<)= auf den Elementen definiert ist,
• und Elemente entsprechend dieser Ordnung platziert sind.

Sortieren

Formale Definition:

Gegeben seien Datenstrukturen d_0, d_1, ...,  d_{n-1} mit Schlüsselwerten s_0, s_1, , s_{n-1} finde eine Permutation pi der Zahlen {0,1,..., n-1} , so dass s_0 <= s_1 <= s_{n-1}

Beim Sortieren sollen selbstverständlich keine Datensätze verändert, gelöscht oder hinzugefügt werden. Für alle Sortieralgorithmen gilt: Das Array a ist jederzeit eine Permutation des ursprünglichen Arrays (Invariante).

Stabiler Algorithmus

• Die Reihenfolge der Elemente mit gleichen Schlüssel werden bewahrt.

In Situ (in place)

• Zusätzlicher Speicherbedarf ist unabhängig von der Anzahl der zu sortierenden Elemente.

Einfache Sortier-Algorithmen

• werden beim Überprüfen eines Arrays Nachbarelemente in falscher Reihenfolge gefunden, so werden sie vertauscht

Bubble-Sort ("Blasen-Sortieren")

• Im ersten Durchlauf wird das Array komplett durchlaufen, das größte Element wandert an seinen Platz am Ende des Arrays
• Beim zweiten Durchlauf geht man nur noch bis zum vorletzten Platz und bringt das zweitgrößte Element dahin, usw. usf.
• In (n-1) . Durchlauf werden nur noch die ersten beiden Elemente verglichen und bei Bedarf vertauscht.
• Verbesserungsmöglichkeit: Man kann aufhören, wenn in einem Durchlauf keine Elemente vertauscht werden.



Aufwand für ein Array der Länge n: (n-1)+(n-2)+...2+1 = n*(n-1)/2 Vergleiche und höchstens genauso viele Vertauschungen.

T(n) = O(n^2) - Bubble-Sort sortiert mit quadratischem Aufwand

weitere einfache Sortierverfahren

• Selection-Sort
• Sortieren durch Auswahl des i. kleinsten Elements für die Position i des Arrays
• Insertion-Sort
• Sortieren durch Einfügen des nächsten Elements in ein bereits sortiertes Teil-Array an der richtigen Stelle
• Auch sie vergleichen im ungünstigsten Fall jedes Element mit jedem Anderen und benötigen daher einen quadratischen Aufwand

 

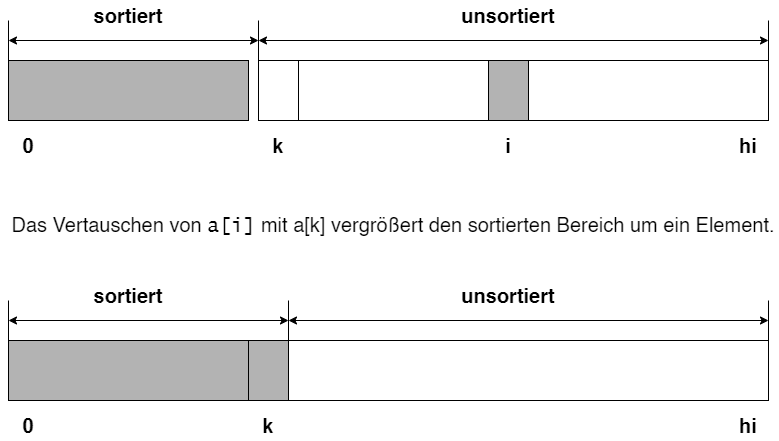
Selection-Sort

• Bei dem Selection-Sort suchen wir in jedem Schritt das kleinste (größte) der noch ungeordneten Elemente und ordnen es am rechten Ende der bereits sortierten Elemente ein.
• In einem Array a mit dem Indexbereich [0...hi] sei k die erste Position und i die Position des kleinsten Elemente im noch unsortierten Bereich.



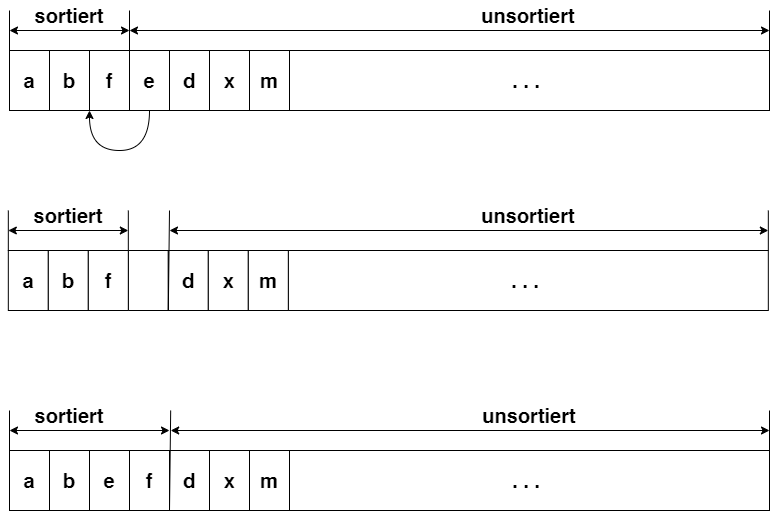
Insertion-Sort

• Nimmt ein beliebiges Element der noch nicht sortierten Daten auf und ordne es an richtiger Stelle ein.
• Element wird aus Liste herausgenommen.

Effiziente Sortieralgorithmen

Erst bei 2^k >= n! ist es möglich, dass alle Teilmengen höchstens eine Permutation enthalten.

Mindestens so viele Vergleiche sind nötig, um auch im ungünstigsten Fall die sortierte Permutation eindeutig zu identifizieren.

2^k >= n! gilt für k >= log_2 n! und nach der Stirling-Formel n! rund -v/2*pi*n *(n/e)^n, n -> ∞ ist

T(n) >= O(n!) = O(1/2 * log_2 2*pi + 1/2 * log_2 n + n*log_2 n - n) = O(n * log_2 n)

Satz:

Jeder Sortieralgorithmus, der nur mit Vergleichen arbeitet, benötigt im schlimmsten Fall (worst case) n * log_2 n Vergleiche, d.h. der Aufwand an Vergleichen ist mindestens von der Ordnung O(n * log_2 n).

Begründung: Die Menge aller n! Permutationen eines Arrays kann aufgeteilt werden durch einen Vergleich in zwei Teilmengen, zwei Vergleiche in vier Teilmengen, usw. k Vergleiche in 2^k Teilmengen.

Solange 2^k < n! ist, gibt es bestimmt noch Teilmengen mit mehr als einer Permutation, d.h., im ungünstigsten Fall ist die sortierte Permutation noch nicht eindeutig identifiziert.

Prinzip „Teile und Herrsche“

• Teile und herrsche („divide et impera“, „divide and conquer“) ist ein allgemeines rekursives Lösungsprinzip für „zerlegbare“ Probleme:

• Falls P „elementar“ lösbar, bestimme Lösung L

• Andernfalls: zerlege Problem P in gleichartige Teilprobleme P_0, P_1, ..., P_n  und löse sie nach dem gleichen Prinzip

• Setze aus den Lösungen L_0, L_1, ..., L_n die Gesamtlösung L von P zusammen

• Vorgehen ist erfolgreich, falls das Zerlegen in kleine Probleme und das Zusammenfügen der Lösungen zur Gesamtlösung effizient gelingen.

Prinzip „Teile und Herrsche“ für Sortieraufgaben

• Sortieren von einelementigen und leeren Arrays ist trivial

• Zerlege größere Arrays in (zwei) kleinere Teil-Arrays

• Sortiere diese Teil-Arrays

• Setze aus den sortierten Teil-Arrays das sortierte Array zusammen

• Bekannte Realisierungen:

• Merge-Sort: „Sortieren durch Mischen“ (J. v. Neumann, 1945)

• Quick-Sort: „Aufteilen in Große und Kleine“ (C. A. R. Hoare, 1962)

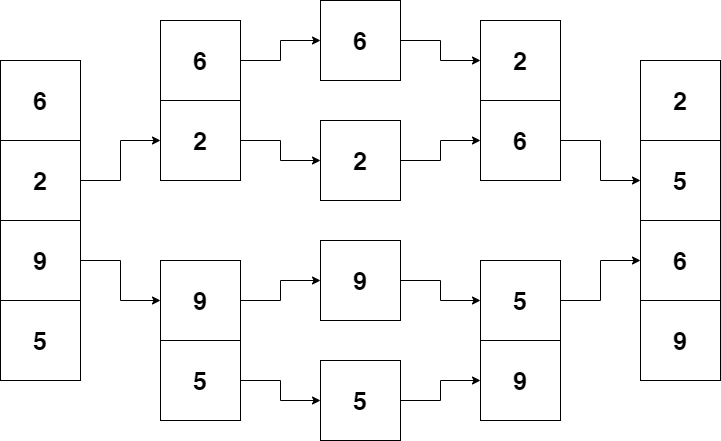
Merge-Sort

• Idee: Teil-Arrays werden als Abschnitte des Arrays zwischen zwei Indizes links und rechts dargestellt.
• (Teil-)Array wird in zwei (annähernd) gleiche Teile geteilt durch Berechnung des Index in der Mitte: mitte = (links + rechts)/2
• Die beiden Teil-Arrays werden sortiert
• Danach werden die sortierten Teil-Arrays in eimen Hilfsarray so gemischt, dass dabei die Sortierung erhalten bleibt.

Nachteil von Merge-Sort: zusätzlicher Speicherplatz von der größe des Arrays erforderlich

Aufwand von Merge-Sort

• Mischen erfolgt durch Vergleich der beiden nächsten noch nicht eingeordneten Elemente.

• Mischen braucht höchstens n-1 Vergleiche und 2*n Umspeicherungen, d.h., erfordert linearen Aufwand in Bezug auf die Gesamtlänge beider Listen.

• Aufwand für ein Array der Länge n ergibt sich aus dem rekursiven Aufruf: T(n) = 2*T(n/2) + (n-1) + 2*n <= 2*T(n/2) + 3*n

Dieser Ausdruck ist von der Ordnung O(n * log2 n).

Quick-Sort

Die Zerlegung des Arrays erfolgt anhand eines Pivot-Elements in zwei TeilArrays:

• Vom linken Rand her sucht man das erste Element des Arrays, das größer oder gleich dem Pivot-Element ist

• Vom rechten Rand her sucht man das erste Element des Arrays, das kleiner oder gleich dem Pivot-Element ist

• Beide Elemente werden vertauscht und der Prozess fortgesetzt, bis man sich irgendwo trifft

• Dort wird das Array geteilt, wobei die Elemente im linken Teil-Array kleiner oder gleich den Elementen im rechten Teil-Array sind

• Schließlich werden die Teil-Arrays sortiert, dann ist das Array als ganzes sortiert

• Die Wahl des Pivot-Elements entscheidet über Aufwand, oftmals wird ein Randelement oder das Mittelelement verwendet

• Entstehen etwa gleich große Teil-Arrays, so ist Aufwand wie bei Merge-Sort O(n*log_2 n)

• Im ungünstigsten Fall (ein Teil-Array enthält nur das Pivot-Element) ist der Aufwand O(n^2)

• Vorteil: Quick-Sort sortiert „in situ“ (in place )und benötigt nur einen zusätzlichen Speicherplatz zum Vertauschen

spezielle Sortierverfahren

• für die spezielle Schlüsseltypen lassen sich Sortierverfahren angeben, die nicht auf dem Vergleichen von Zahlen oder Objekten beruhen, sondern auf Verteilen und Wiederaufsammeln.
• Für Werte aus Bereichen der ganzen Zahlen:
• Sortieren durch Zählen des Vorkommens (Count-Sort)
• Für Zeichenfolgen fester Länge:
• Sortieren durch Verteilen in Fächer (Radix-Sort)

Count-Sort (Sortieren durch  Zählen)

Sortieren durch Zählen des Vorkommens für Werte-Bereiche ganzer Zahlen

• Durch Verschieben ist immer eine Transformation auf einen Bereich nicht negativer ganzer Zahlen möglich

• Daher betrachten wir nur das Sortieren von Arrays nicht negativer ganzer Zahlen

• Man zählt in einem Hilfsarray, wie oft jede Zahl in dem zu sortierenden Array vorkommt, entsprechend oft schreibt man die Zahl zurück

• Größe des Hilfsarrays ergibt sich aus dem Maximum der zu sortierenden Werte

• Falls keine Abschätzung dieses Maximums bekannt ist, so ermittelt man es durch n-1 Vergleiche, d.h., mit linearem Aufwand

• Auch zum Zählen der Vorkommen der Werte genügt das einmalige Durchlaufen des Arrays

• Das Zurückschreiben erfordert ebenfalls nur so viele Schritte, wie Array-Elemente vorhanden sind

• Sortieren durch Zählen gelingt daher mit linearem Aufwand O(n)

Radix-Sort

Sortieren von Zeichenfolgen einer festen Länge durch Verteilen auf Fächer

• Jedes mögliche Zeichen erhält eigenes Fach

• Für jede Stelle der Zeichenfolgen findet ein eigener Verteilungslauf und ein anschließender Sammellauf statt (für die „niedrigste“ Stelle zuerst, für die „höchste“ zuletzt)

• Beim Verteilungslauf für die Stelle i wird die Zeichenfolge auf das Fach für das Zeichen an dieser Stelle verteilt

• Beim anschließenden Sammellauf werden die Zeichenfolgen aus den Fächern entnommen unter Beibehaltung ihrer relativen Reihenfolge

Gemischte/Hybride Sortierverfahren

Tim-Sort

• benannt nach Tim Peters
  

• abgeleitet aus Merge-Sort und Insertion-Sort
  

• stabiles Verfahren
  

• best case: O(n)
  

• average/worst case: O(n*log(n)
  

 

Das Java-Collections-Framework

• Definiert eine einheitliche Architektur zur Darstellung und Bearbeitung von Sammlungen

Eine "Collection" ist ein Behälter (Container) zur Verwaltung von Objekten

• Beispiele: Arrays, Vector, Hashtable (in Java seit JDK 1.0 vorhanden)
  

• weitere Datenstrukturen sind z.B. Stapel, Warteschlangen, Wörterbücher, Mengen, Listen, Bäume, usw., die unterschiedlich implementiert werden können.

Dafür steht seit JDK 1.2 im Paket java.util ein umfangreiches "Collection-Framework" aus Interfaces, Implementierungen und Algorithmen zur Verfügung.

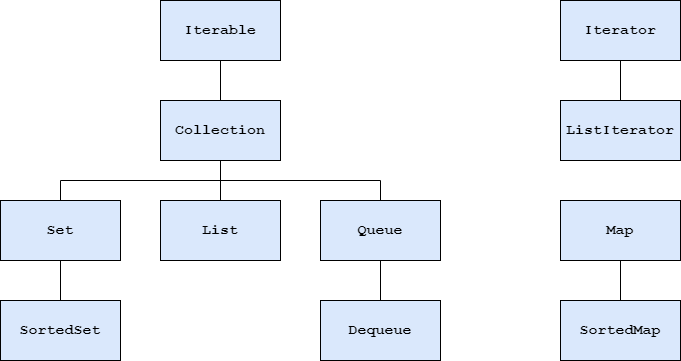
Durch eine Reihe von Interfaces werden häufig verwendete abstrakte Datentypen beschrieben:




 

Vorteile

• Mit dem Framework können viele Aufgaben mit viel weniger Programm-Code erledigt werden

Alphabetisches Sortieren einer String-Liste:

• Collection.sort(liste);

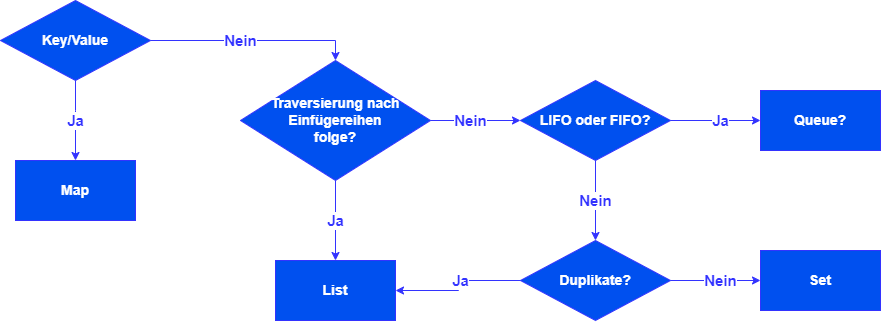
Interface Interable

• Iteratoren ermöglichen den einfachen Zugriff auf jedes Element einer Collection - Die darunterliegende Datenstruktur wird versteckt

Vereinbart die Existenz eines Iterators:

  public interface Iterable{
  	Iterator iterator();
  }

• Interface iterator definiert Methoden zum Traversieren von Behältern:

  public interface Iterator{
      boolean hasNext();
      E next();
      void remove(); //optional
      //löscht zuletzt zurückgegebenes Element
  }

 

Java-Collection-Framework - Überblick

Iterable

• stellt durch iterator()-Methode einen Iterator zur Verfügung

Collection

• definiert allgemeine Methoden für Behälter

Iterator

• definiert Methoden zum Traversieren (Durchlaufen) eines Behälters

ListIterator

• definiert Methoden zum Traversieren einer Liste in beide Richtungen

List

• definiert Methoden für Behälter mit Elementen in einer bestimmten Reihenfolge, auf die über ihre Positionsnummer zugegriffen werden kann

Set

• definiert Methoden für Behälter ohne doppelte Elemente und ohne bestimmte Reihenfolge (Mengen im mathematischen Sinn)

SortedSet

• definiert Methoden für Mengen mit einer Ordnung der Elemente (definiert durch Comparablebzw. Comparable)

Queue

• definiert Methoden für Warteschlagen-Behälter, deren Elemente nach bestimmten Regeln eingefügt und nur vorn entnommen werden können

Deque: Double-Ended QUEue

• definiert Methoden für Warteschlangen-Behälter, deren Elemente an beiden Enden nach der LIFO-Regel ("last in - first out") eingefügt und entnommen werden können (quasi ein zwei-seitiger Stapel)

Map

• definiert Methoden für Abbildungs-Behälter, in denen Schlüssel-Wert-Paare gespeichert werden können, wobei keinen doppelten Schlüssel erlaubt sind (Abbildungen im mathematischen Sinn)

SortedMap

• definiert Methoden für Abbildungs-Behälter mit einer Ordnung für die Schlüssel-Elemente (definiert durch Comparable bzw. Comparator)

 

Zu den Interfaces gibt es eine Reihe von Standard-Implementierungen

• List: ArrayList, LinkedList (Vektor)
• Queue: LinkedList, PriorityQueue
• Deque: LinkedList, ArrayDeque
• Set: HashSet, LinkedHashSet
• SortedSet: TreeSet
• Map: HashMap, LinkedHAshMap, (Hashtable)
• SortedMap: TreeMap
• für eigene Implementierungen gitb es abstrakte Klassen zum Ablweiten
• für spezielle Anforderungen existieren Spezial-Implementierungen

 




 

Hashing

Beispiele für Hash-Tabellen

• Memory-Management: Tabelle im Betriebssystem
• Symbol-Tabellen für Computer
• Environment-Variablen (Unix)

Begriffsbestimmung

• Hashing (engl. to hash = zerhacken): Aufteilen der gesamten Schlüsselmenge
• Die Position eines Daten-Elementes im Speicher ergibt sich (zunächst) durch Berechnung direkt aus dem Schlüssel (Key).
• Datenstruktur = häufig lineares Array der Größe m (Hashing-Tabelle)

Prinzip des Hashing

• R = Raum (Universum) aller möglichen Schlüssel
  
• S = Menge von Schlüsseln (Keys), die aktuell in Hash-Tabelle abgelegt sind wobei |S| = n gilt
  
• Beobachtung: Wenn R sehr groß ist, ist ein Array für R nicht handhabbar.
• In der Praxis ist |S| << |R|
• Idee: Benutze eine Tabelle, deren Größe in etwa in der selben Größenordnung wie |S| ist
• Einträge in solch einer Hashing-Tabelle nennt man Slots.

Hash-Funktion

Wie muss eine Funktion aussehen, die die Schlüssel auf die Slots der Hash-Tabelle abbildet?

Hash-Funktion h : bildet Schlüssel aus R auf Slots einer Tabelle T[0..m-1] ab

• Beim normalen Array: Schlüssel s wird abgebildet in den Slots A[s]
• Bei Hash-Tabellen: Schlüssel s wird abgebildet in den Slot T[h(s)] - man sagt auch s hashes to ...

h(s) wird auch als Hash-Wert oder Hash-Adresse des Schlüssels s bezeichnet


 

Beispiele einer einfachen Hash-Funktion

h(k) = m*(k*A% *1) = m*(k*A - k*A)

(k*A - k*A) in [0,1]

m*(k*A - k*A) in [0,1,..., m-1]

A im Intervall [0,1) -> Vorschlag von D.E. Knuth: A = -v/5-1/ 2

 

Hash-Tables in Java

• Wird der vorgegebene Ladefaktor überschritten, so vergrößern Hash-Map bzw. Hash-Table-Objekte ihr Speicher-Array und die Hash-Tabelle wird neu aufgebaut

Kapazität von Hash-Tabellen

• Kapazität der Hash-Tabelle: Größe des Arrays
• Ladefaktor: Anzahl der zu speichernder Daten/Kapazität
• Beide Werte können bei der Erzeugung von HashMap- bzw. HashTable-Objekten vorgegeben werden
• Erfahrungswert: bis Ladefaktor 0,75 sind Kollisionen bei guten Hash-Funktionen selten
• Dann haben die meisten Listen des Arrays nicht mehr als ein Element und beim Zugriff auf Daten muss nur selten gesucht werden.
• Zugriffsaufwand für Daten bleibt meist konstant.

 

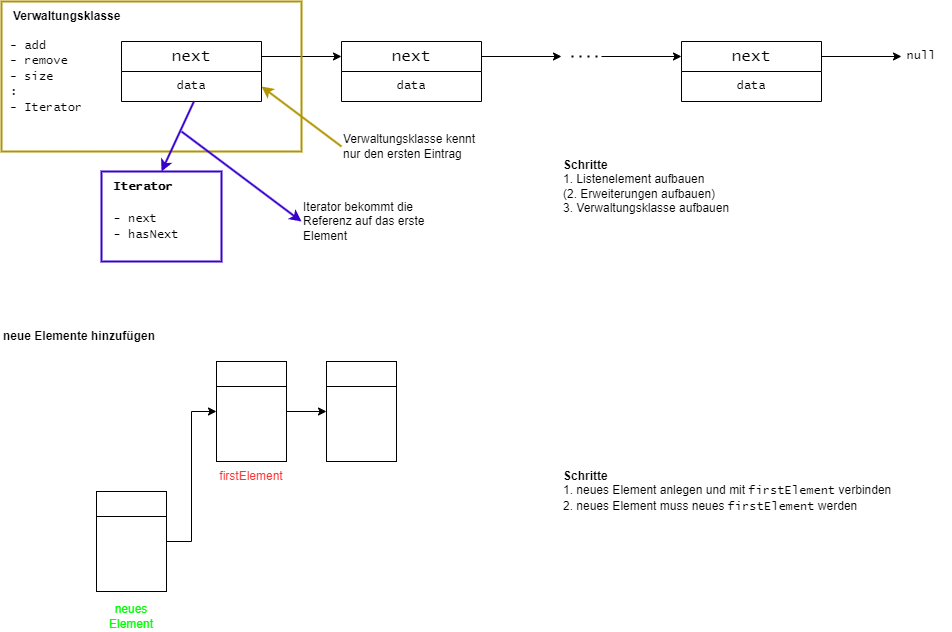
Einfach verkettete lineare Listen

Grundbaustein ist eine rekursive Datenstruktur "Listen-Element" (Knoten) besteht aus

• data Dateninhalt und
• next Verweis auf das nächste Listenelement

Grundlegende Operationen:

• Test auf leere Liste
• Lesen
• Einfügen
• Löschen
• ...

Aneinanderreihung von Listen-Elementen

• Zugriff durch Verweis auf erstes Element
• Ende der Liste erkennbar an "leerem Verweis" auf das nächste Element
• Operationen über gesamte Liste sind möglich
• in rekursiver Form
• in iterativer Form

 

Einfach verkettete Listen

einfach verkettete Listen sind als Stapel geeignet

• effiziente Arbeit am Listenanfang
• aber: ineffiziente Arbeit am Listenende, gesamte Liste muss durchlaufen werden
• nur sequentielle Suche möglich
• einfach verkettete Listen wurden deshalb verschiedenartig aufgebaut und erweitert
• einfach verkettete Liste mit Referenzen auf das erste und letzte Element
• doppelt verkettete Liste mit erstem und letztem Hilfselement oder als Ringliste
• LinkedList des Java-Collection-Framework ist als doppelt verkettete Ringliste realisiert

 




 

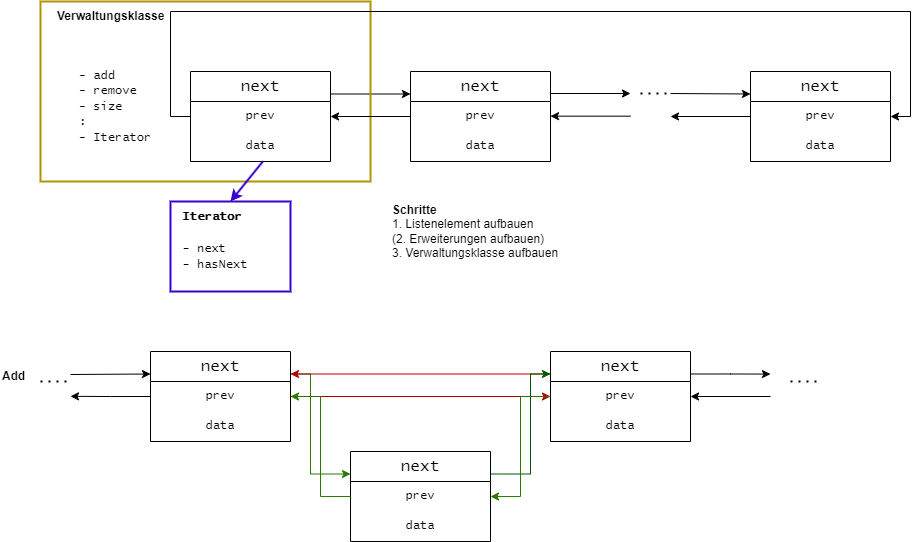
Doppelt verkettete Listen

Grundbaustein: Listenelement aus

• data Dateninhalt
• next Verweis auf das nächste Listenelement
• prev Verweis auf das vorhergehende Element

Doppelt verkettete Ringliste mit Eintrittselement Vereinbarungen:

• Dateninhalt null ist unzulässig (außer beim Eintrittselement)
• Listenlänge wird (redundant) als Attribut gespeichert

 

Vorteile

• Einfügen am Ende sehr viel schneller möglich, kein Durchlaufen der ganzen Liste (geht natürlich auch bei einfacher Liste, falls Referenz auf Ende mitgeführt wird)

Nachteile

• höherer Speicherbedarf - zwei Referenzen pro Listenelement
• höherer Aufwand bei Manipulation der Liste



 

Bibliotheken in Java

• Erweiterung der Funktionalität von Java
• Bibliotheken umfassen in der Regel einen speziellen Bereich
• Qualität der Bibliotheken schwankt sehr stark -> keine genauen Richtlinien vorhanden

 

Beispiele:

• Testen von Java-Anwendungen
• grafische Anwendungen
• (Fehler-) Berichterstattung
• Abfrage von externen Quellen (Datenbanken, JSON, ...)

 

Apache Commons

• Erweiterungen um viele Funktionen zur einfachen Arbeit in Java

Google Guava

• von Google entwickelt

Erweiterung von Bibliotheken:

• StringHelper -> schnell toString()-Methoden schreiben
• ComparisonChain -> schnell eine compareTo()-Methode schreiben (inkl. Verkettung)
• diverse Mathematik-Funktionen wie GGT, ... und bsp. BigInteger

JSON

• -> Javascript Object Notation
• kompakter als XML
• primär für Webanwendungen und Apps
• Dateien sind lesbar für Mensch und Maschine

⚠nicht jede Programmiersprache unterstützt JSON von Haus aus ⚠

JSON - Datentypen

• Nullwert
• Boolean
• Zahl
• Zeichenkette
• Array
• Objekt
• Erweiterungen nur begrenzt vorhanden

 

JSON - Beispiel

  {"employees":[
  	{"firstname": "Linus", "lastname": "Torvaldis"}
  	{"firstname": "James", "lastname": "Gosling"}
  	{"firstname": "Ken", "lastname": "Thompson"}
  ]}

XML

• -> eXtensible Markup Language
• sehr stark erweiterbare Auszeichnungssprache (-> Markup Language)
• wird durch das W3C (World Wide Web Consortium) verwaltet

Anwendungsfelder:

• Websites
• Grafik
• Web Services
• Konfigurationen
• ...

XML-Dateien sind lesbar für Mensch und Maschine

XML-Programmierschnittstelle:

• DOM
• SAX
• ...

Spezifikationen von XML

• gibt Anordnung (Reihenfolge, Verschachtelung, ...) von Tags vor
• Tags können i.d.R frei bzw. aufs Fach bezogen benannt werden
• Die Semantik (Inhalt) ist sehr flexibel
• Die Syntax (Grammatik) ist sehr streng
• Beachtung von:
• Wohlgeformtheit (stimmt die Grammatik)
• Gültigkeit (stimmt der Inhalt)

 

XML Elemente und Attribute

Element (tag):

• kann bebliebig (auch keine) Kind-Elemente haben und/oder Attribute

leeres Element:

• enthält keine Kind-Elemente und Attribute

root-Element:

• ist nur einmal im XML-Dokument enthalten und umfasst alle

DOM

• -> Document Object Model
• gesamtes XML-Dokument wird eingelesen
• Elemente, Attribute, usw. werden als Interface bzw. abstrakte Klassen abgebildet
• Definition unabhängig von der Programmiersprache
• genaue Definition unter: https://www.w3.org/dom

SAX

• -> Simple API for XML
• Event-basiert
• nicht offizieller W3C-Standard
• -> StAX

XSLT

• -> eXtensible Stylesheet Language Transformation
• Transformation von XML-Dokumenten in ein neues Dokument

XPath

• XML Path Language

XML vs. JSON

	XML	JSON
Sprache	Markup Language	"nur" ein Format
Speicherung	Baumform	Map
Verarbeitung	Verarbeitung in diversen Formen (PDF, HTML, ...)	-
Geschwindigkeit	langsam	schnell
Erweiterungen	vorhanden (z.B. FMXL)	bedingt vorhanden
Größe	sehr schnell ansteigend	nicht schnell ansteigend
Datentypen	Erstellung eigener Datentypen	"nur" String, Numbers, Arrays, Boolean und Objekte

Datenbanken

JDBC Bibliotheken

• Java Database Connectivity
• Reihe von Bibliotheken zur Verbindung mit Datenbanken
• keine universelle Bibliothek vorhanden
• Je Datenbank -> eine Bibliothek
• teilweise Zusammenfassung



 

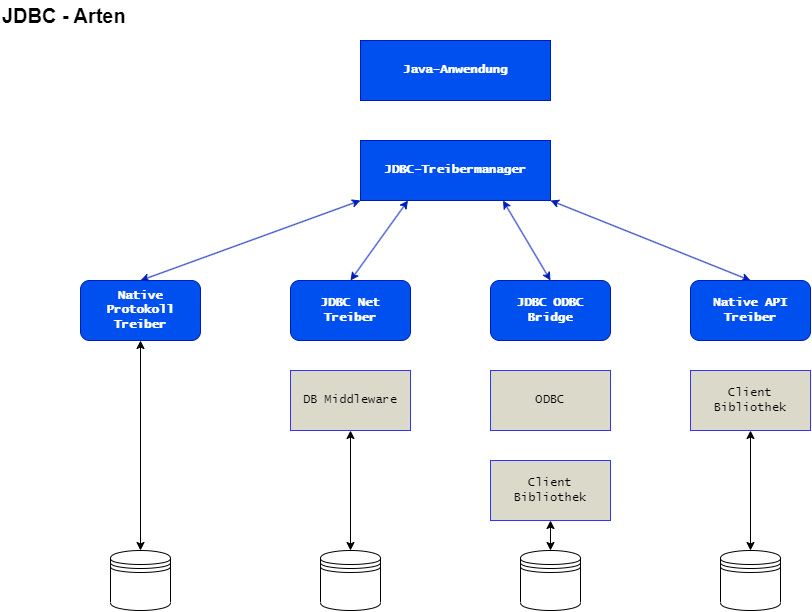
Java und Datenbanken

1. Aufbau einer Verbindung zur Datenbank über einen Verbindungsmechanismus -> Datenbank-abhängig
2. Senden einer SQL-Anweisung
3. Verarbeiten der Anfrageergebnisse
4. Freigeben der Ressourcen

Bäume

• Bäume sind nichtlineare Datenstrukturen für flexibles und effizientes Einfügen, Löschen oder Suchen

Bäume werden in der Informatik an vielen Stellen verwendet, um Daten in einer hierarchischen Ordnung zu verwalten

• Datei- und Prozess-System in UNIX
• Klassenhierarchie objektorientierter Sprachen
• Syntax-Bäume
• Datenspeicherung in Datenbank-Systemen

Können aus ähnlichen Grundelementen wie verkettete Listen aufgebaut werden

Grundbegriffe

• Die Länge des Weges von der Wurzel zu einem Knoten heißt "Tiefe", ("Ebene", "Niveau") des Knotens (Wurzel hat Tiefe 0)
• Die größte Knoten-Tiefe in einem Baum heißt die "Höhe" des Baumes
• Wenn den Knoten eines Baumes ein Wert zugeordnet ist, heißt dieser Wert eine "Marke" und der Baum ein "markierter Baum"
• In der Informatik geht es i.a. um markierte Bäume, in deren Knoten Daten bzw. Datenstrukturen enthalten sind



 

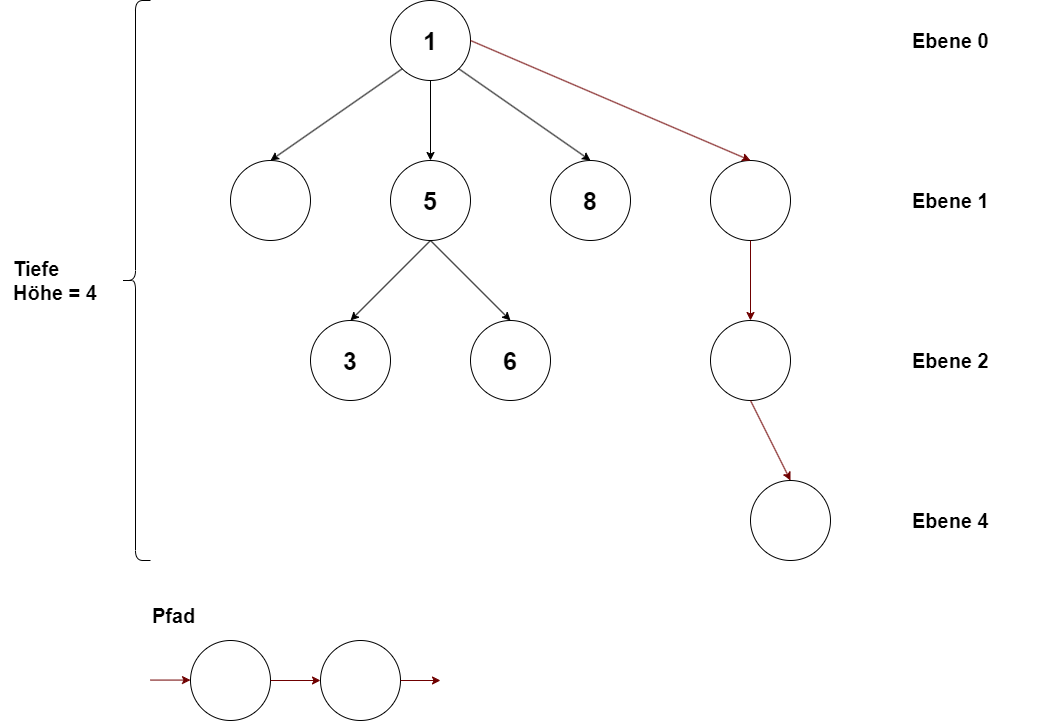
Grundbegriffe II

• Vorgängerknoten eines Knotens heißen auch "Eltern(-knoten)" oder "Vater(-knoten)"
• Nachfolgerknoten eines Knotens heißen auch "Kind(-knoten)"
• Kantenfolgen heißen "Pfad" oder "Weg", ihre Länge ist die Anzahl der Kanten bzw. ist die Anzahl der Knoten - 1
• "Teilbaum" ("Unterbaum") heißt jeder Teil eines Baumes, der selbst ein Baum ist
• Ein Knoten ohne Nachfolger heißt ein "Blatt"
• Alle anderen Knoten sind "innere Knoten"

Grundbegriffe III

• gerichtete Graphen bestehen aus:

Knoten und Kanten,

• jede Kante führt von einem Vorgängerknoten zu einem Nachfolgerknoten

Bäume sind spezielle Graphen:

• haben einen speziellen Knoten:
• die "Wurzel"
• außer Wurzel hat jeder Knoten genau einen Vorgängerknoten
• von der Wurzel aus führt zu jedem Knoten genau eine Kantenfolge.

 

Huffmann-Baum

• auch Huffmann-Kodierung

Entropiekodierung (verlustfreie Datenkompression)

 




 

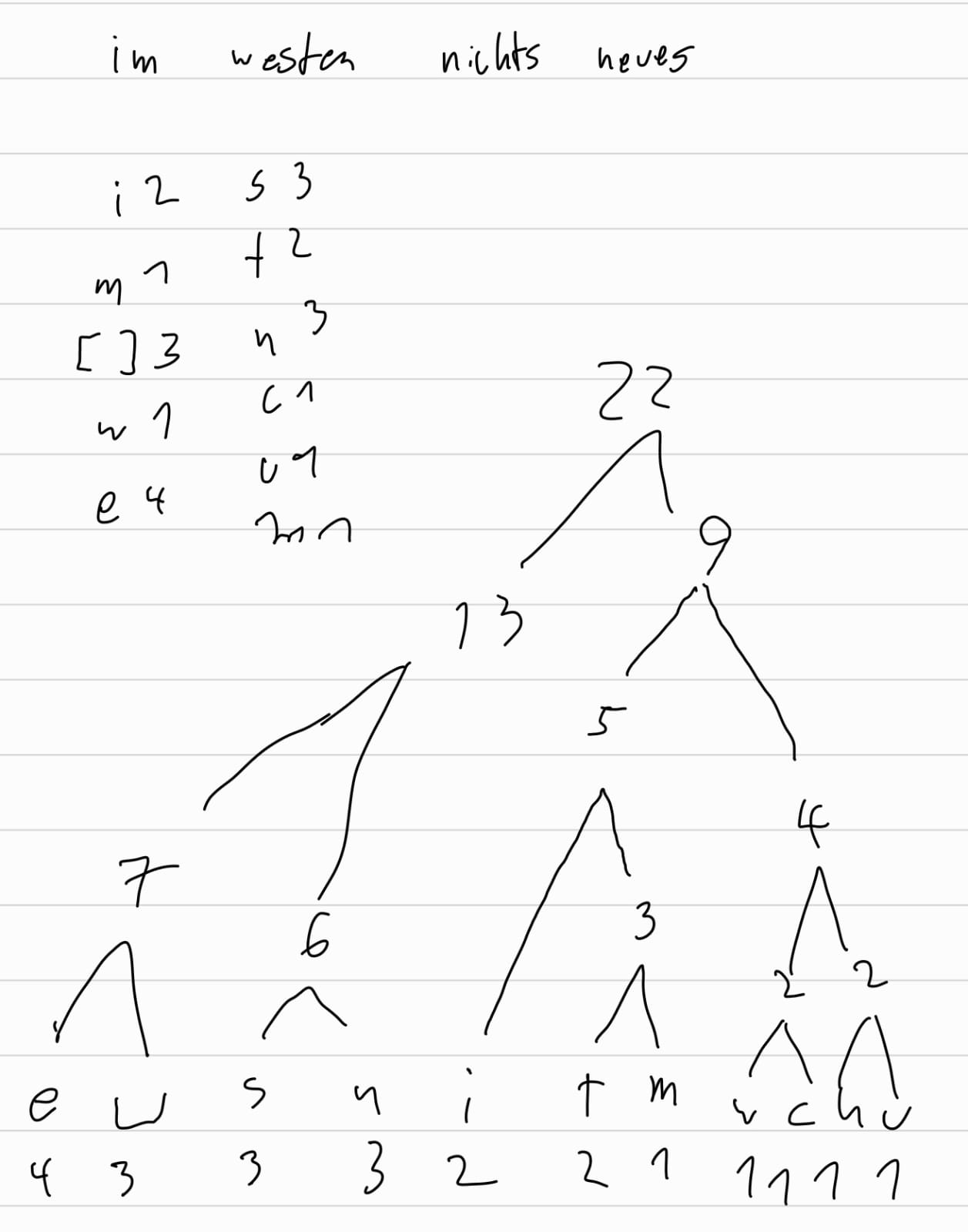
Traversierung

• -> systematisches Durchlaufen der Knoten, dafür sind unterschiedliche Strategien möglich:
• Strategie PreOrder ("Vorordnung"):
• Verarbeite die Wurzel
• Verarbeite den linken Teilbaum
• Verarbeite den rechten Teilbaum
• Strategie InOrder ("Inordnung"):
• Verarbeite den linken Teilbaum
• Verarbeite die Wurzel
• Verarbeite den rechten Teilbaum
• Strategie PostOrder ("Nachordnung"):
• Verarbeiten den linken Teilbaum
• Verarbeite den rechten Teilbaum
• Verarbeite die Wurzel

 

Darstellungsmöglichkeiten

• Analog zu Listen werden die zu speichernden Datenstrukturen durch Referenzen auf
• Nachfolgerknoten und/oder Vorgängerknoten ergänzt, die die Kanten darstellen
  
• Bei speziellen Baum-Strukturen können die Datenstrukturen auch in Arrays gespeichert werden, wobei Indizes anstelle von Referenzen verwendet werden
  

Problem: variable Anzahl von Nachfolgerknoten erfordert i.a. ein Array von Referenzen

Ausweg: Darstellung mit zwei Referenzen "linkes Kind" und "rechte Geschwister"

 

Binäre Bäume

• sind Bäume, deren Knoten höchstens zwei Nachfolgeknoten haben, wobei zusätzlich zwischen "linkem" und "rechtem" Nachfolger unterschieden wird

Beispiele:

• Term-Bäume für zweistellige Operationen
• Bäume in Darstellung mit linkem Kind und rechten Geschwistern

 

Binäre Bäume - Datenstrukturen

• einfachste Form verwendet als Grundelement eine Darstellung
• der Knoten als Datenstruktur
• aus Dateninhalt und Verweisen
• auf rechten und linken Nachfolgerknoten

Eine Verknüpfung solcher Elemente ergibt einen binären Baum, der durch einen Verweis auf den Wurzelknoten zugänglich wird

 

Binäre Suchbäume

Ein binärer Baum heißt binärer Suchbaum, wenn für jeden Knoten gilt:

• Die Dateninhalte in den Knoten seines linken Teilbaums sind alle kleiner als sein Dateninhalt.
  

• Die Dateninhalte in den Knoten seines rechten Teilbaums sind alle größer oder gleich als sein
  Dateninhalt.
  

 

Binäre Suchbäume - Wurzel löschen

Spezialfall des Löschens von Daten erfodert die Unterscheidung von drei Fällen:

• linker Teilbaum ist leer: Wurzel ersetzen durch Wurzel des rechten Teilbaums
• rechter Teilbaum ist leer: Wurzel ersetzen durch Wurzel des linken Teilbaums
• beide Teilbäume nicht leer: Aus rechtem Teilbaum Knoten mit minimalem Dateninhalt löschen, Dateninhalt in Wurzel übernehmen (analog wäre das Löschen des Maximums aus linkem Teilbaum möglich)

 

Graphen in der Informatik

Ein Graph besteht aus einer Knotenmenge V (Vertex) und einer Kantenmenge E (Edge)

Unterscheidung in:

• gerichteter Graph -> Graph  G = (V, E); E c_ V x V
• ungerichteter Graph -> Graph  G = (V, E);  E c_ P(V), P(V) alle 2-elementigen Teilmengen von V
• Gewichtung der Kanten



 

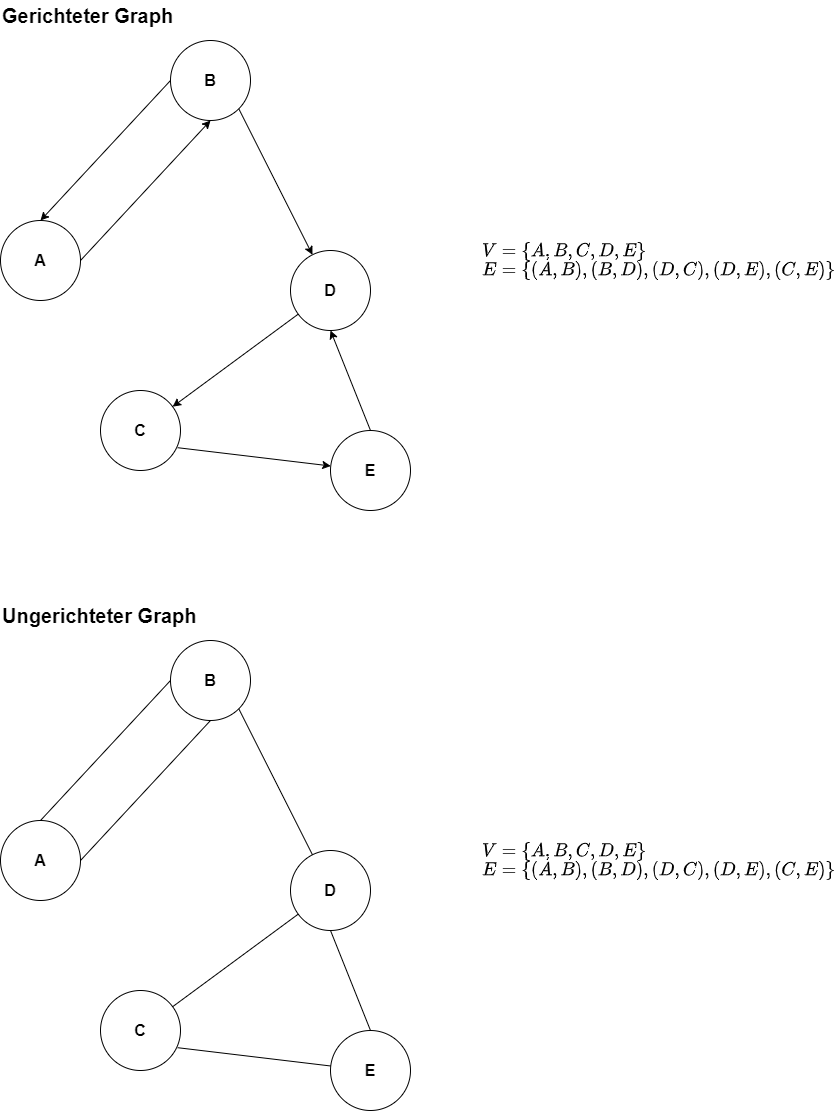
Graphen_Grundbegriffe.png

MST

• Minimal (Minimum) Spanning Tree
• Kanten sind gewichtet

Teilbaum des Graphen

• ist verbunden
• azyklisch
• alle Knoten sind enthalten

Algorithmen zur Bestimmung:

• Prim
• Kruskal
• Boruvka

 

Graphen Repräsentation

Kanten-Menge

• Angabe der Anzahl von Knoten und Kanten
• Paarung von Knoten, welche verbunden sind

Matrix

• Matrixschreibweise für die Knoten

Listen

• Jeder Knoten enthält eine Liste von verbundenen Knoten

 

Matrix Repräsentation

verwende ein 2-dimensionales Knoten-zu-Knoten boolsches Feld bzw. Integer-Feld

• -> auch Adjazenzmatrizen genannt

Jede Kanten (v-w) innerhalb des Graphen wird über adj[v][w] = adj[w][j] = true abgebildet

Boolean oder Integer als Datentyp?

• Integer bei Gewichtung
• ∞ -> Integer.MAX_INTEGER

 

Wegsuche nach Dijkstra

Behauptung: Der Dijkstra-Algorithmus findet gaqrantiert den kürzesten Pfad von einem Punkt S aus.

Beweis:

• Jede Kante e = v \: \rightarrow w genau einmal aufgespannt (von Knoten v aufgespannt wurde),
• Dabei gilt: In der Datenstruktur
• DisTo[w] <= DisTo[v] + e.weight().
• Die Ungleichung bleibt weiter gültig, bis der Algorithmus beendet ist, da:
• DisTo[w]

  nicht weiter anwachsen kann ( DisTo[] Werte sind monoton fallend)
  

• DisTo[v]

  wird sich nicht ändern, da wir in jedem Schritt die niedrigsten DisTo[]-Werte wählen
  

• Per Definition alle Kantengewichte nicht negativ sind.

Schlussfolgerung: Die Bedingung für den kürzesten Pfad bleibt erhalten bis der Algorithmus terminiert.

Der Dijkstra-Algorithmus scheint vertraut?

• -> Prim-Algorithmus ist im Wesentlichen der gleiche Algorithmus

Hauptunterscheid: Wie der nächste Knoten für den Spannbaum bestimmt wird:

• Prim: Nächster Knoten zum Baum (über eine ungerichtete Kante)
• Dijkstra: Nächster Knoten der am nächsten zum Startpunkt ist (über einen gerichteten Weg)



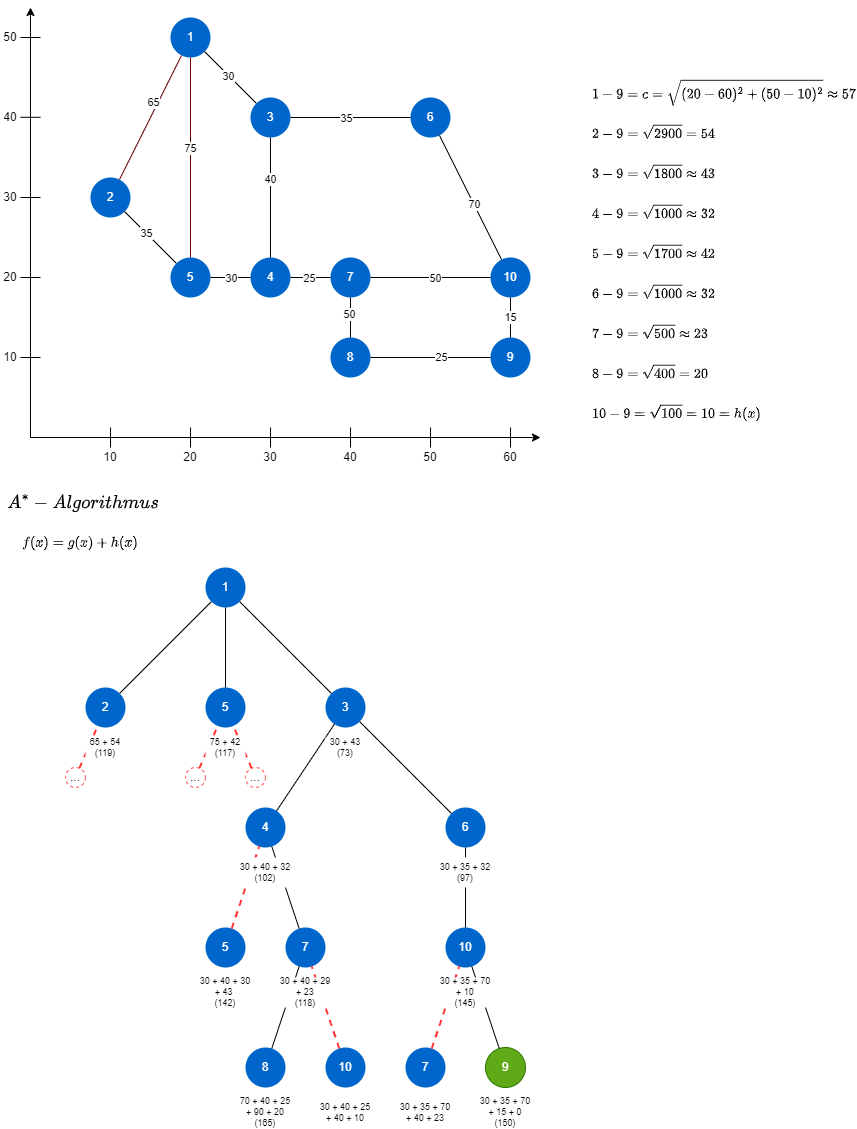
Rucksackproblem

1- n Objekte mit Gewicht g_1 - g_n und Wert w_1 - w_n

 

Backtracking

• Backtracking (Rückverfolgung) ist einer der allgemeinsten Alorithmenentwurfstechniken. Sie beruht auf dem Prinzip "versuche etwas, und wenn es nicht klappt, versuche etwas anderes".
• Um backtracking anwenden zu können, muss die gewünschte Lösung als n -Tupel (x_1, ..., x_n) darstellbar sein, wobei

 

Dynamische Programmierung

Das dynmische Programmieren ist eine Methode zum Entwurf von Algorithmen, die man dann anwenden kann, wenn die Lösung